启发式优化求解之插值网络迭代
1 前言
很多工程问题(比如图优化、深度学习、数据拟合、方程组求解、组合优化……),涉及到数学建模,然后求解。数学算法建模是一种能力的体现,绝大部分人只关注建模,而对模型求解器底层的开发因其小众而被"忽视"。在业余时间里,喜欢测试并改写各种求解器算法,以期待从中找到某种数学可解释的规律,进而开发出一种求解效果较好的求解器。
工程中求解的问题,往往非凸,对于非凸求解,成熟的凸优化算法显得力有不足。启发式优化算法这时应运而生。遗憾的是,不少构造的启发式优化算法,不以数学规律去进行算法构造,而是以仿生方式强行对公式进行解释,似乎一个算法加上一个生物的名字就显得智能而高大,个人不建议这样做。当然,这里不否认,有一些仿生的启发式求解算法效果不差!
在这里,不以仿生解释,尽量从数学知识方面,“胡说八道”一把启发式优化算法迭代公式。
2 插值网络
2.1 约定
这里约定求解的模型为单目标无约束模型,因此最终可以等价为优化如下目标
(1)
$$
\mathbf{min}:f(\mathbf{x})
$$
公式里\(f\)为模型函数,\(\mathbf{x}\)为求解变量。
在求解器里,每一个可能的解称为节点,每个节点上有对应求解的变量值和度量值。假如求解器里有\(m\)组节点(种群),第\(i\)个节点上的变量值和度量值分别为\(\mathbf{x}_i、y_i\),其中变量的维度为\(n\),则它们有如下关系
(2)
$$
y_i=f(\mathbf{x_i})
$$
2.2 理论
在某个迭代次里,已经知道了这\(m\)组各个节点上的\((\mathbf{x}_i,y_i)\)。这里参照数值分析篇里关于插值理论章节的知识,对于一个未知模型,如果要插值出某个未知点的值,可以通过已知点的信息按经验插值出这个未知点附近的高概率值。而这个经验是什么呢,就是当一个点分布在已知物理点时附近时,它们距离越近其物理属性相似的概率越大。因此这里,设插值节点的变量为\(\mathbf{\bar{x}}\),对应的度量值为\(\bar{y}\),这时需要构建一个插值网络模型,使得\(\mathbf{\bar{x}}\)与\(\mathbf{x}_i\)越近,\(\bar{y}\)与\(y_i\)一致的概率越大,那这里可以构建如下插值网络模型
(3)
$$
\begin{cases}
\bar{f}(\mathbf{x}) &= \dfrac{1}{m\alpha}\sum_{i=1}^m(\alpha – ||\mathbf{\bar{x}}-\mathbf{x}_i||^2)y_i
\\
\\
\alpha &=\sum_{i=1}^m||\mathbf{\bar{x}}-\mathbf{x}_i||^2
\end{cases}
$$
上面模型虽然并不一定过每个节点,但是其不违背插值经验,这样构建的模型本质属于概率统计的菜系。
这里构建函数的目的是使得模型函数\(\bar{f}(\mathbf{x})\)去相似\(f(\mathbf{x})\),前者看似对后者进行了简化,实则还是有些复杂。为了进一步简化,这里将\(\alpha\)看做一个常量(变量冻结,在优化当中是一种有效的处理手段)。当然,从另一个方面看这个常量: 在每次迭代中,总可以找到一个常量\(\alpha\)使得其满足在求解域内为如下值
(4)
$$
\alpha = \mathbf{max}(\sum_{i=1}^m||\mathbf{\bar{x}}-\mathbf{x}_i||^2)
$$
由于\(\alpha\)为常量,因此\(\bar{f}(\mathbf{x})\)模型变成了凸模型,要求其极值点,对于\(j=1,2,..,n\)。令导数为0有
(5)
$$
\begin{aligned}
\dfrac{\partial \bar{f}}{\partial \bar{x}_j}&=-\dfrac{2}{m\alpha}\sum_{i=1}^m(\bar{x}_j-x_{ij})y_i=0
\\
&\Downarrow
\\
\bar{x}_j&=\dfrac{\sum_{i=1}^mx_{ij}y_i}{\sum_{i=1}^my_i}
\end{aligned}
$$
公式里\(\bar{x}_j\)表示\(\mathbf{\bar{x}}\)的第\(j\)个元素,\(x_{ij}\)表示第\(i\)个节点上变量值第\(j\)个元素。
因此最终(5)里的\(\mathbf{\bar{x}}\)就是需要寻找的节点变量更新迭代式。搞了半天,没弄出复杂得让人膜拜(复杂)的手抄,就弄出这么一个看似小儿科的公式,大道至简,也许就是这样!
2.3 进阶
设有单调递增函数\(g(x)\),对(1)构造等价目标函数
(6)
$$
\mathbf{min}:g(f(\mathbf{x}))
$$
很明显,(1)和(6)有相同的极值点,因此对于(5)构造如下的节点变量更新
(7)
$$
\begin{cases}
w_i &=g(y_i)
\\
\\
\bar{x}_j&=\dfrac{\sum_{i=1}^mx_{ij}w_i}{\sum_{i=1}^mw_i}
\end{cases}
$$
从上面公式可以看出,迭代方向随着函数映射方式不同而有所改变。进一步,仔细观察可以发现,(5)的迭代式是(7)里\(g(x)=x\)的特例。
另外,当\(\beta\)取一个非常大的常数,且\(g(x)\)取如下表达式时
(8)
$$
g(x)=\exp(x+\beta)
$$
这时(7)的变量更新将变为如下形式
(9)
$$
\mathbf{\bar{x}}\approx \dfrac{1}{m}\sum_{i=1}^m\mathbf{x}_i
$$
公式(9)就是我们常见的多组节点变量取平均格式。
当然,在实际使用时,根据度量值的大小,也可以考虑使用《两个新的带符号缩放函数》
(10)
$$
\begin{cases}
g(x) &= \mathbf{logSign}(x)
\\
g(x) &= \mathbf{expSign}(x)
\end{cases}
$$
2.4 注意
在实际使用时,注意以下几点:
① 设定\(g(x)\)函数,不同的函数形式结果有所差异,这可以作为算法改进的一个突破点
② 选择指定范围内的节点使用公式(7)得到新的节点变量
③ 在新节点变量周围进行局部凸求解
④ 最小化目标函数\(f(\mathbf{x})\)的值设计为非负
3 应用
3.1 集成
这里基于上面的理论开发了两个新算法:
① INS求解器(插值网络求解器),迭代中只使用上面理论进行变量更新。算法已经集成到开源框架《HeuristicSolver 》,具体参看INSSolve.h文件
② ISWO求解器(基于插值网络改进的SWO求解器), 在SWO求解迭代中追加上面理论更新策略。算法已经集成到开源框架《HeuristicSolver 》,具体参看ISWOSolver.h文件
3.2 算法评价
在对求解器算法评价时,总会以统一的方式去评价各个求解器优劣。虽然约定的评价方式无法精确反映求解器好坏,但可以大致反映求解器的能力。这里约定如下方式评价:
① 所有求解器用同函数、同维度、同初值。
② 在同硬件配置,同环境里测试,且以时间来控制最大迭代次数,即每次求解的总时间不超过设定值。
③ 相同函数对每个求解器设置的随机加偏一致。
④ 多轮迭代,取最好一次度量值以及中位数度量值作为最终得分参考指标。
注意:
(1) 常规的评价方式里对②使用迭代次数进行限制,这种方式有非常大的缺陷。因为不同方法设计的求解器,同一轮迭代,实际也可能多次调用函数,或者裹挟有各种复杂计算,这样造成有些迭代一次很快,有些迭代一次需要等半天,这明显不公平。在实际问题求解中,更关注求解器在多少时间内能达到什么水平,因此在求解器算法对比中用耗时来控制最大迭代次数显得更加合理。
(2) 对于第③点,如果测试函数最优解在某值附近(比如常见的0值),为了防止设计的求解器算法对这类特解有偏好,可以看成一种作弊,因此对测试函数输入随机加偏不失为一种“防作弊”的有效手段。
3.3 例子
下面选了几个比较典型的例子进行测试(前两个函数是自己筛选求解器算法的必测函数),所有测试函数均可以在开源框架《HeuristicSolver 》里找到。下面的算例均控制最大迭代时间为3分钟,节点数量设置为90。
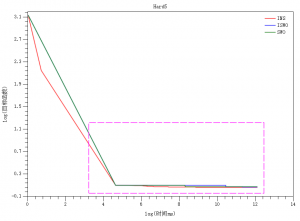
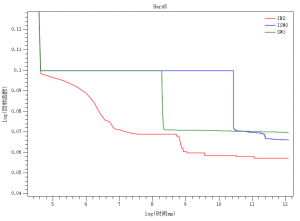
3.3.1 Hard5案例
来源: 文献[1]里的第一个例子
维度: 5
其它: 图中时间与目标函数均取了对数
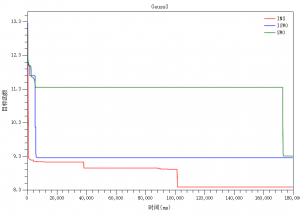
3.3.2 Gauss3案例
来源: 文献[2]里的Gauss3函数
时间: 3分钟
其它: 图中目标函数取了对数
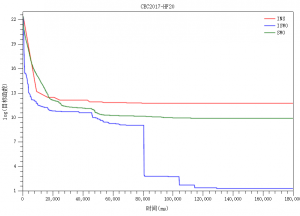
3.3.3 CEC2017-HF20案例
来源: 文献[3]里的HF20函数
维度: 1000
加偏: 函数统一随机加偏
其它: 图中目标函数取了对数
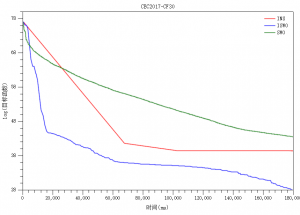
3.3.4 CEC2017-CF30案例
来源: 文献[3]里的CF30函数
维度: 1000
加偏: 函数统一随机加偏
其它: 图中目标函数取了对数
参考:
[1] 程培澄,程培聪,王萌,等.非线性方程组求解器全局优化求解能力对比研究[J].计算机应用与软件, 2022, 39(10):1-10.DOI:10.3969/j.issn.1000-386x.2022.10.001.
[2] 美国国家标准与技术研究院(NIST)提供的测试函数.
[3] Problem Definitions and Evaluation Criteria for the CEC 2017 Special Session and Competition on Single Objective Real-Parameter Numerical Optimization.