分类： 未分类

多种相机模型

shikang999 评论

现今相机传感器使用广泛，为了使相机成像更加真实，就需要了解对应相机模型以及对应参数，进而修复可能出现的成像问题。了解模型后，采用对应模型进行相机标定，然后去畸变等等。

 

1 针孔相机

1.1 针孔相机模型

对于薄透镜的针孔相机，其成像可简化成如下形式

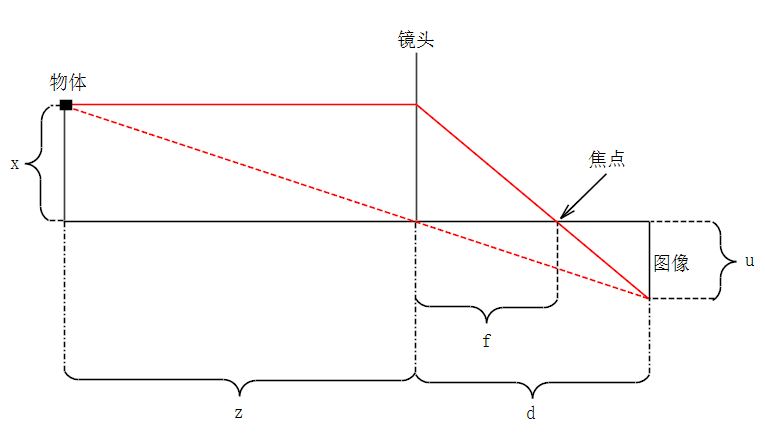
上面模型中，\((x,y,z)\)为相机坐标系下的3D点，其中以相机镜面正前方为\(z\)方向。上面模型中\(f\)为相机焦距，\(d\)为像距。根据相似三角形原理，不难得到如下结果

(1)$$ \begin{cases}
\dfrac{x}{f}=\dfrac{u}{d-f}
\\
\dfrac{x}{z}=\dfrac{u}{d}
\end{cases}
\Rightarrow f=\dfrac{d}{\dfrac{d}{z}+1} \Rightarrow \dfrac{1}{f}=\dfrac{1}{z}+\dfrac{1}{d}
$$

受限于相机尺寸以及为了扩大成像视野，一般\(z >> d\)，这时\(f \approx d\)(这就是成像在焦点附近比较清晰的原因)，因此可得到像平面的坐标

(2)$$ 
p_x=f\dfrac{x}{z}
$$

同理可以得到

(3)$$ 
p_y=f\dfrac{y}{z}
$$

注意，\((p_x, p_y)\)仅是理论上像平面的坐标。由于相机一般由感光器件来进行图像映射，感光器反馈的是像素单元的坐标，假设单个像素横向占用\(1/l_x\)米，纵向占用\(1/l_y\)米，则可以使用\(l_x、l_y\)将\((p_x, p_y)\)缩放到像素坐标。另一方面，由于\((p_x, p_y)\)得到的坐标是以相机光心为原点，而常见的图像坐标以图像左上角为原点，因此需要移动原点，这时在缩放后的像素坐标上加一个偏移\((c_x,c_y)\)。一般\((c_x,c_y)\)取相机光心在像素中的坐标值。最终有如下针孔相机模型

(4)$$ \begin{cases}
u =l_xp_x+ c_x= f l_x \dfrac{x}{z}+c_x
\\
v =l_yp_y + c_y =  f l_y \dfrac{y}{z} + c_y
\end{cases}
$$

为了简洁表示，这里设归一化坐标\((x',y')\)如下

(5)$$ \begin{cases}
x'=\dfrac{x}{z}
\\
y'=\dfrac{y}{z}
\end{cases}
$$

以及设置内参

(6)$$ \begin{cases}
f_x =f l_x
\\
f_y = f l_y
\end{cases}
$$

将(5)(6)代入(4)得有针孔相机模型

(7)$$ \begin{cases}
u = f_x x'+c_x
\\
v =f_y y' + c_y
\end{cases}
$$

 

1.2 图像倾斜修正

现在面阵相机比较普遍，工业上也使用线阵相机，而有些线阵相机也会按线条进行拼接成一个“面阵”，因此最终都需要呈现矩阵像素点阵。如下图a，理想中的相机传感器上的感光器件应该呈方形(或矩形)分布，然而对于一些生产工艺较差的相机，如下图b，其感光器件可能呈现如下右图的平行四边形排布。当出现图b的情形时，这时呈现的图像也跟着倾斜。如果想了解一些成像原理，可以参考文献[1]。

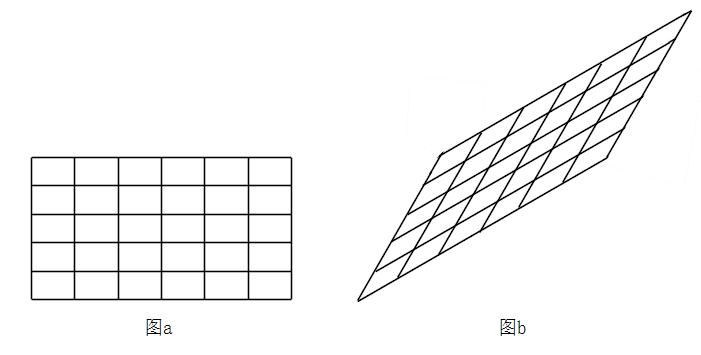
为了解决上图倾斜的问题，不失一般性，以上图b为原型，建立如下图的模型。

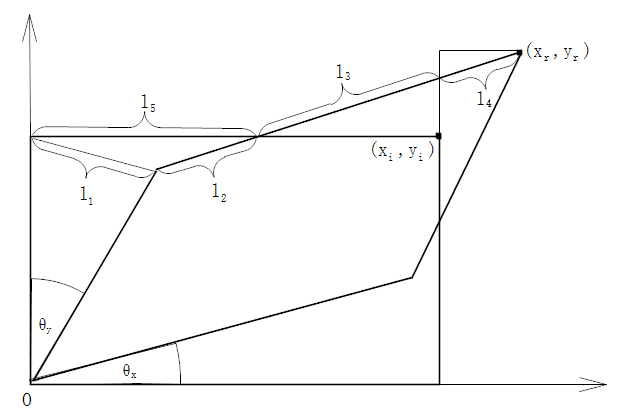
这个模型中约定真实成像点应该在\((x_r,y_r)\)，因为感光器原因，反馈了一个错误的位置\((x_i,y_i)\)，器件沿着\(x\)轴倾斜的角度为\(\theta_x\)，沿着\(y\)轴倾斜角度为\(\theta_y\)，这时需要得到模型中的坐标\((x_r,y_r)\)。根据模型中的几何关系，可以得到

(8)$$\begin{aligned}&\begin{cases}
\dfrac{l_1}{\sin\theta_y}=\dfrac{y_i}{\sin(\dfrac{\pi}{2}-\dfrac{\theta_y}{2})}
\\
\dfrac{l_1}{\sin \theta_x}=\dfrac{l_2}{\sin\dfrac{\theta_y}{2}}=\dfrac{l_5}{\sin(\pi-\theta_x-\dfrac{\theta_y}{2})}
\\
l_3=\dfrac{x_i-l_5}{\cos \theta_x}
\\
l_4=x_i-l_2-l_3\\
x_r =x_i+l_4\cos\theta_x
\\
y_r = y_i+(l_3+l_4)\sin\theta_x
\end{cases}\\ &\Downarrow
\\&\begin{cases}
x_r =\cos\theta_xx_i+\sin\theta_yy_i
\\
y_r =\sin\theta_xx_i+\cos\theta_y y_i
\end{cases}\end{aligned}
$$

注意，上面公式中\((x_i,y_i)\)与\((x_r,y_r)\)都不是相对相机光心像素点为原点，进一步这里设置\(S\)矩阵

(9)$$S =\begin{bmatrix}
\cos\theta_x & \sin\theta_y
\\
\sin\theta_x & \cos\theta_y
\end{bmatrix}
$$

将(9)代入(8)有

(10)$$ \begin{aligned}
\begin{bmatrix}
x_r
\\
y_r
\end{bmatrix}
&=S\begin{bmatrix}
x_i
\\
y_i
\end{bmatrix}
\\
&=S\begin{bmatrix}
f_xx'+c_{xi}
\\
f_yy'+c_{yi}
\end{bmatrix}
\\
&=S\begin{bmatrix}
f_xx'
\\
f_yy'
\end{bmatrix}+S\begin{bmatrix}
c_{xi}
\\
c_{yi}
\end{bmatrix}
\\
&=S\begin{bmatrix}
f_xx'
\\
f_yy'
\end{bmatrix}+\begin{bmatrix}
c_x
\\
c_y
\end{bmatrix}
\\
&=\begin{bmatrix}
fl_x\cos\theta_x & fl_y\sin\theta_y
\\
fl_x\sin\theta_x & fl_y\cos\theta_y
\end{bmatrix}\begin{bmatrix}
x'
\\
y'
\end{bmatrix}+\begin{bmatrix}
c_x
\\
c_y
\end{bmatrix}
\end{aligned}
$$

公式(10)中的\((c_x,c_y)\)表示修正后的偏移量。进一步，为了简洁表示，这里设置如下变量

(11)$$\begin{cases}
f_x = fl_x\cos\theta_x
\\
f_y=fl_y\cos\theta_y
\\
\alpha_x =fl_x\sin\theta_x
\\
\alpha_y=fl_y\sin\theta_y
\end{cases}$$

设置如下内参矩阵\(K\)

(12)$$K = \begin{bmatrix}
f_x & \alpha_y & c_x
\\
\alpha_x & f_y & c_y
\\
0 & 0 & 1
\end{bmatrix}$$

则可得倾斜修正后的模型

(13)$$ \begin{bmatrix}
u
\\
v
\\
1
\end{bmatrix}=K \begin{bmatrix}
x'
\\
y'
\\
1
\end{bmatrix}$$

注意，内参矩阵\(K\)里的参数\(f_x、f_y、\alpha_x、\alpha_y\)反映了各自缩放与倾斜的信息，特别地，当\(\alpha_x = 0\)时，内参矩阵\(K\)变为如下形式

(14)$$K = \begin{bmatrix}
fl_x & fl_y\sin\theta_y & c_x
\\
0 & fl_y\cos\theta_y & c_y
\\
0 & 0 & 1
\end{bmatrix} = \begin{bmatrix}
f_x & \alpha_y & c_x
\\
0 & f_y & c_y
\\
0 & 0 & 1
\end{bmatrix}=\begin{bmatrix}
f_x & \alpha f_x & c_x
\\
0 & f_y & c_y
\\
0 & 0 & 1
\end{bmatrix}$$

公式(14)中\(\alpha = \dfrac{l_y}{l_x}\sin\theta_y\)，OpenCV中就使用的这种表示形式，由于一般\(l_x\)与\(l_y\)值很接近，因此\(\alpha \approx \sin\theta_y\)，这时\(\alpha\)主要反映阵列偏离\(y\)轴的程度，这个值越远离0，则越加倾斜。

 

PS:

A : 上面导出的修正模型中\(\theta_x、\theta_y\)正负均可，导出的公式一致。

B : 这里的导出方式和一般文献的导出方式正好相反(例如文献[2])，这里基于的原理是给相机一个非矩形正确的光源点位置，但是信号反馈到一个矩形错误的位置，因此对其进行修正，而一般的文献推导是正确的光源点为矩形位置，信号反馈为非矩形位置。

C : 现今的相机，一般\(\theta_x=0、\theta_y=0\)，所以很多时候\(K\)少了\(\alpha_x、\alpha_y\)两个内参。

D ：常规情况下，认为工艺中仅存在左右倾斜的情况，即\(\theta_x=0\)，所以大部分文献导出的内参没有\(\alpha_x\)。

E :  常规情况下，\(l_x \approx l_y\)，所以大部分情况下会看到\(f_x\)与\(f_y\)接近。

 

1.3 针孔相机畸变

1.2修正的是倾斜，倾斜的模型是线性的，而有时成像扭曲，这时就需要对相机进行畸变处理。

由于相机装配或者本身形状原因，相机图像一般存在畸变，畸变呈现的图形往往扭曲。

1.3.1 径向畸变

由透镜形状引起的畸变称为径向畸变，在透镜拍摄过程中，往往一条直线在相机上显示为一条曲线，在越靠近边缘的地方，这种现象越明显。这里径向畸变主要包括桶形失真(图形上表现为外凸)与枕形失真(图形上表现为内凹)。

由于径向畸变是随着与中心之间的距离增加而增加，因此往往使用一个与径向相关的多项式来进行修正：

(15)$$
\begin{cases}
x_d=x'(1+k_1r'^2+k_2r'^4+k_3r'^6+…)
\\
y_d=y'(1+k_1r'^2+k_2r'^4+k_3r'^6+…)
\end{cases}
$$
公式中\(k_1,k_2,k_3,…\)表示修正系数，一般的相机使用\(k_1,k_2\)修正系数就足够了，而对于鱼眼相机可能还需要加入\(k_3\)作为修正项。这里径向半径 \(r'=\sqrt{x'^2+y'^2}\)。

 

1.3.2 切向畸变
由于相机组装过程中不能使透镜和成像面严格平行，这时会引入切向畸变，对于切向畸变，可使用如下公式修正  
(16)
$$
\begin{cases}
x_d=x'+2p_1x'y'+p_2(r'^2+2x'^2)
\\
y_d=y'+p_1(r'^2+2y'^2)+2p_2x'y'
\end{cases}
$$

1.3.3 针孔相机畸变修正模型
结合(15)(16)得到针孔相机畸变的修正模型  
(17)
$$
\begin{cases}
x_d=x'(1+k_1r'^2+k_2r'^4+k_3r'^6+…)+2p_1x'y'+p_2(r'^2+2x'^2)
\\
y_d=y'(1+k_1r'^2+k_2r'^4+k_3r^6+…)+p_1(r'^2+2y'^2)+2p_2x'y'
\end{cases}
$$

使用修正后的归一化坐标\((x_d,y_d)\)代入(13)的相机模型有

(18)$$
 \begin{bmatrix}
u
\\
v
\\
1
\end{bmatrix}=K \begin{bmatrix}
x_d
\\
y_d
\\
1
\end{bmatrix}
$$

 

1.4 针孔相机内参标定

所谓内参标定，就是通过某种方式确定出内参矩阵\(K\)以及相应的畸变参数。而这里所谓的某种方式，就是在已知输入输出的情况下，反算出内参，这里涉及到两个层面：非线性求解、给定输入输出。

非线性求解，这个需要使用非线性求解器，这里直接采用某种非线性求解算法即可。

给定输入输出，即现实中给定某个特征，这个特征成像后具有某种性质，而根据这种性质建立约束，进而使用非线性方法迭代求解。例如直线特征，现实生活中一条直线，成像后也应该是一条直线，而不是曲线；现实生活中不是特远的矩形块儿，成像后也应该保持矩形特征。所以常见使用方形格子标定板进行标定。当然，也可以不使用方形格子板，自己手动指定一些特征，也是一样的。

还需要注意的是，如果标定时夹杂了位姿(一个变换),如果能提前确定好位姿值最好，否则优化求解中会多位姿变量的求解。这个主要根据构建约束的方式来确定。

 

2 其它相机模型

这里提到的相机模型，均需要去畸变，它们主要不同点是去畸变基于的模型不同。去完畸变后，就简化成一个针孔相机，进而成像。

这里同样记物点在相机坐标系下坐标为\((x,y,z)\)，归一化坐标为\((x',y')\)，下面的模型主要是对\((x',y')\)修正得到\((x_d,y_d)\)，最后代入(18)式。因此每个模型中的内参除了模型需要的几个参数外，还包括\(K\).

 

2.1 UCM模型[3]

UCM模型全称叫Unified Camera Model。这个模型主要用于折反射相机。它是基于一个物点投影到单位球体上，然后再投影到像平面这么一个过程构建模型。这个模型的修正公式如下

(19)$$
\begin{cases}
x_d=\dfrac{x}{\alpha d + (1-\alpha)z}
\\
\\
y_d=\dfrac{y}{\alpha d + (1-\alpha)z}
\end{cases}
$$

公式中\(\dfrac{\alpha}{1-\alpha}\)表示球体中心到像平面距离，而\(d\)则使用如下方式计算

(20)$$d = \sqrt{x^2+y^2+z^2}$$

UCM模型需要的内参为\(K, \alpha\).

 

2.2 EUCM模型[3]

EUCM模型全称叫Extended Unified Camera Model。UCM的镜头是一个圆形球面，为了更具一般性，EUCM将镜头模型扩展到椭圆形，因此增加了一个控制椭圆程度的参数\(\beta\)(此参数越接近1，镜头椭圆度越小，这时镜头面越接近圆球面；否则镜头的椭圆度越大，镜头面就是椭圆面了).

EUCM模型依然使用(19)式进行修正，但\(d\)则使用如下方式计算

(21)$$d = \sqrt{\beta(x^2+y^2)+z^2}$$

EUCM模型需要的内参为\(K, \alpha, \beta\).

 

2.3 KB模型[4]

KB模型全称叫KannalaBrandt Camera Model，它是Juho Kannala和Sami S. Brandt根据几种鱼眼模型(等距投影模型、等立体角投影模型、正交投影模型和体视投影模型)分析得出。KB模型是一个通用模型，适合常见的普通镜头、广角镜头、鱼眼镜头。这个模型的修正公式如下

(22)$$
\begin{cases}
x_d=\dfrac{\theta_d}{r}x
\\
\\
y_d=\dfrac{\theta_d}{r}y
\end{cases}
$$

公式中的\(r, \theta_d\)使用如下公式获取

(23)$$\begin{aligned}
r &= \sqrt{x^2+y^2}
\\
 \theta &=\arctan(r,z)
\\
\theta_d&=\theta+k_1\theta^3+k_2\theta^5+k_3\theta^7+k_4\theta^9+…
\end{aligned}$$

KB模型需要的内参为\(K, k_1, k_2, k_3, k_4, …\).

 

2.4 FOV模型[3]

FOV模型全称叫Field Of View Camera Model。FOV(视场相机)模型, 假设像点与主体点之间的距离近似正比于对应的3D点与光轴之间的角度，因此提出如下修正模型

(24)$$
\begin{cases}
x_d=\dfrac{r_d}{r}x
\\
\\
y_d=\dfrac{r_d}{r}y
\end{cases}
$$

公式中\(r_d\)按如下方式计算

(25)$$r_d=\dfrac{\arctan(2r\tan(w/2), z)}{w}$$

公式中的参数\(w\)表示对应于理想鱼眼镜头的视场。

FOV模型需要的内参为\(K, w\).

 

2.5 DS模型[3]

DS模型全称叫Double Sphere Camera Model，即双球面相机模型。这个模型主体思想是，一个点会被连续投影到两个球体上。这个模型可以看成EUCM的扩展。作者说这个模型更加适合鱼眼相机。这里模型的修正公式如下

(26)$$
\begin{cases}
x_d=\dfrac{x}{\alpha d_2+(1-\alpha)(\xi d_1+z)}
\\
\\
y_d=\dfrac{y}{\alpha d_2+(1-\alpha)(\xi d_1+z)}
\end{cases}
$$

公式中\(d_1、d_2\)按如下方式计算

(27)$$\begin{aligned}d_1 &= \sqrt{x^2+y^2 + z^2}
\\
d_2&=\sqrt{x^2+y^2+(\xi d_1 + z)^2}\end{aligned}$$

公式中\(\xi\)反映了两个单位球体中心的偏移量。

因此DS模型需要的内参为\(K, \alpha, \xi\).

 

参考

[1] 吴建明. 全面详细解析CMOS和CCD图像传感器

[2] 吕泽乾. 数字图像相关中相机标定技术及其应用拓展[D]. 2020, 中国科学技术大学.

[3] Usenko V , Demmel N , Cremers D . The Double Sphere Camera Model: IEEE, 10.1109/3DV.2018.00069[P]. 2018.

[4] Kannala J , Brandt S S . A generic camera model and calibration method for conventional, wide-angle, and fish-eye lenses[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2006, 28(8):1335.

对极约束-2D点对匹配建立相机间相对测量约束

shikang999 评论

1 约定
这里约定对于一个3D点位置为\(\mathbf{p}\)，其坐标为(\(x,y,z\))，则\(\mathbf{p}\)采用如下齐次坐标表示  
(1-1)
$$
\mathbf{p}'=\begin{bmatrix}
\mathbf{p}
\\
1
\end{bmatrix}=\begin{bmatrix}
x
\\
y
\\
z
\\
1
\end{bmatrix}
$$
对于相机内参\(K\)，约定\(K'\)其为如下4\(\times\)4齐次矩阵  
(1-2)
$$
K'=\begin{bmatrix}
K & \mathbf{0}
\\
\mathbf{0}^T & 1
\end{bmatrix}=\begin{bmatrix}
K_{00} & K_{01} & K_{02} & 0
\\
K_{10} & K_{11} & K_{12} & 0
\\
K_{20} & K_{21} & K_{22} & 0
\\
0 & 0 & 0 & 1
\end{bmatrix}
$$
对于相机位姿\(T\)，这里约定的表示为世界坐标到相机坐标的变换，其满足如下定义  
(1-3)
$$
T=\begin{bmatrix}
R & \mathbf{t}
\\
\mathbf{0}^T & 1
\end{bmatrix}
$$

对于相机平面上的像素位置(\(u,v\))，深度为\(s\) ，用点 \(\mathbf{g}\)表示，其坐标形式为  
$$
\mathbf{g} = \begin{bmatrix}
u
\\
v
\\
1
\end{bmatrix}
$$

对于元素个数为1的向量，其表示形式与数值等价。


2 理论

2.1 问题
在空间中有个3D点 \(\mathbf{p}\)在相机1(位姿为\(T_1\))的里的像素位置为\(\mathbf{g}_1\)以及深度值为\(s_1\) ，\(\mathbf{p}\)在相机2(位姿为\(T_2\))的里的像素位置为\(\mathbf{g}_2\)以及深度值为\(s_2\)。现在想建立相机1与相机2之间的相对测量信息。

2.2 相对测量
两个相机位姿间的相对测量不应该随着同一个刚体变换而改变，根据(1-3)的约定，这里两个相机的相对测量\(T\)使用如下定义  
(2-1)
$$
T = T_1T_2^{-1}
$$

注意：这里的相对测量是定义在整体刚体变换情况下，相对测量不变的基础上。也就是说，不管怎么移动，他们之间的相对测量值不再改变。

2.3 已知推导
根据2.1的信息有  
(2-2)
$$
\begin{cases}
s_1\begin{bmatrix}
\mathbf{g}_1
\\
1/s_1
\end{bmatrix}=K_1'T_1\mathbf{p}'
\\
\\
s_2\begin{bmatrix}
\mathbf{g}_2
\\
1/s_2
\end{bmatrix}=K_2'T_2\mathbf{p}'
\end{cases}
\Rightarrow
s_1K_1'^{-1}\begin{bmatrix}
\mathbf{g}_1
\\
1/s_1
\end{bmatrix}=T_1T_2^{-1}(s_2K_2'^{-1}\begin{bmatrix}
\mathbf{g}_2
\\
1/s_1
\end{bmatrix})=T(s_2K_2'^{-1}\begin{bmatrix}
\mathbf{g}_2
\\
1/s_1
\end{bmatrix})
$$
展开上面公式有  
(2-3)
$$
s_1K_1^{-1}\mathbf{g}_1=R(s_2K_2^{-1}\mathbf{g}_2)+\mathbf{t}
$$
上面公式中的\(R\)与\(t\)来自\(T\)。进一步，这里设如下中间变量  
(2-4)
$$
\mathbf{a}_1=K_1^{-1}\mathbf{g}_1
\\
\mathbf{a}_2=K_2^{-1}\mathbf{g}_2
$$
将(2-4)带入公式(2-3)有  
(2-5)
$$
\begin{aligned}
s_1\mathbf{a}_1&=s_2R\mathbf{a}_2+\mathbf{t}
\\
\Downarrow
\\
s_1 \mathbf{t}^\wedge\mathbf{a}_1&=s_2 \mathbf{t}^\wedge R \mathbf{a}_2
\\
\Downarrow
\\
s_1\mathbf{a}_1^T\mathbf{t}^\wedge\mathbf{a}_1&=s_2\mathbf{a}_1^T\mathbf{t}^\wedge R \mathbf{a}_2
\end{aligned}
$$
因为\(\mathbf{a}_1^T\mathbf{t}^\wedge\mathbf{a}_1 = 0\)，因此代入(2-5)可以得到如下表达式  
(2-6)
$$
\mathbf{a}_1^T\mathbf{t}^\wedge R \mathbf{a}_2 = 0
$$
因此，最终公式(2-6)就是我们导出的2D匹配点间相机间相关测量约束关系。

需要特别注意的是，(2-6)公式存在缺陷，如果使用这个约束作为优化的边，需要谨慎。

仔细观察(2-6)可以发现，当\(\mathbf{t}=\mathbf{0}\)时，\(R\)取任意值，均满足上面的表达式，很明显，这种满足无穷组特解的模型对优化有一定误导作用。针对这种情况，需要增加有意义的约束，这里设\(\mathbf{t}=\mathbf{0}\)，代入公式(2-5)可得到如下形式  
(2-7)
$$
\mathbf{a}_1^\wedge R \mathbf{a}_2=\mathbf{0}
$$
因此，当\(\mathbf{t}=\mathbf{0}\)时，直接使用公式(2-7)作为约束。

2.4 解的限定

虽然(2-6)与(2-7)给出了限定的约束条件，但这时使用的边依然存在多解的情况，而这些多解中有些并不满足实际的条件。在实际使用中，只有深度\(s_1,s_2\)为正数，才符合我们预期，因此可以将这个判定条件，进一步加入约束。这里设置如下变量

(2-8) $$
\begin{aligned}
\mathbf{b} &=\mathbf{a}_1
\\
\mathbf{c} &=R\mathbf{a}_2
\end{aligned} $$

根据公式(2-5)，在\(||\mathbf{t}||_2^2 > 0\)时有

(2-9)
$$
s_1\mathbf{b}=s_2\mathbf{c}+\mathbf{t}
$$

求解(2-9)有

(2-10)$$
\begin{cases}
s_1&=\dfrac{t_2c_0-t_0c_2}{b_2c_0-b_0c_2}=\dfrac{t_2c_1-t_1c_2}{b_2c_1-b_1c_2}=\dfrac{t_1c_0-t_0c_1}{b_1c_0-b_0c_1}
\\
s_2&=-\dfrac{b_0t_2-b_2t_0}{b_0c_2-b_2c_0}=-\dfrac{b_1t_2-b_2t_1}{b_1c_2-b_2c_1}=-\dfrac{b_0t_1-b_1t_0}{b_0c_1-b_1c_0}>0
\end{cases} $$

根据(2-10)可得到如下等效判别式

(2-11)

$$\begin{cases}
(t_2c_0-t_0c_2)(b_2c_0-b_0c_2)>0
\\
(t_2c_1-t_1c_2)(b_2c_1-b_1c_2)>0
\\
(t_1c_0-t_0c_1)(b_1c_0-b_0c_1)>0
\\
(b_0t_2-b_2t_0)(b_0c_2-b_2c_0)<0
\\
(b_1t_2-b_2t_1)(b_1c_2-b_2c_1)<0
\\
(b_0t_1-b_1t_0)(b_0c_1-b_1c_0)<0
\end{cases}$$

对于\(||\mathbf{t}||_2^2 = 0\)时，这时公式(2-5)变成

(2-12)

$$
\begin{aligned}
\dfrac{s_1}{s_2}\mathbf{b}&=\mathbf{c}
\\
&\Downarrow
\\
\dfrac{s_1}{s_2}&=\dfrac{c_0}{b_0}=\dfrac{c_1}{b_1}=\dfrac{c_2}{b_2}>0
\end{aligned}
$$

根据(2-12)可得到如下等效判别式

(2-13)$$\begin{cases}
b_0c_0>0
\\
b_1c_1>0
\\
b_2c_2>0
\end{cases}$$

因此，当使用(2-6)算式约束时,使用(2-11)作为辅助判别约束；当使用(2-7)算式约束时，使用(2-13)作为辅助判别约束。

空间直线匹配建立相关约束

shikang999 评论

1 空间中两条直线匹配建立关系
现在已知空间直线A方程为  
(1)
$$
\mathbf{p}_1 = \mathbf{n}_1\alpha + \mathbf{p}_1'
$$

现在已知空间直线B方程为  
(2)
$$
\mathbf{p}_2 = \mathbf{n}_2\beta + \mathbf{p}_2'
$$

上面公式中\(\mathbf{n}_1\)为直线A单位方向向量，\(\mathbf{n}_2\)为直线B单位方向向量。现在将直线A进行(\(R,\mathbf{t}\))变换后，能与直线B完全重合。现在想建立直线A、B、以及(\(R,\mathbf{t}\))的关系。

构建关系有多种方式，比如将线上变换后的点到目标线的距离作为约束；另一种法方式是将变换后的点投到目标线参数方程上, 如果点在线上，则满足参数方程约束。本文建立关系则基于后一种方式。

1.1 考虑方向向量匹配
有时，我们能够确定直线A与直线B在A通过(\(R,\mathbf{t}\))变换后,其变换后的直线与直线B完全重合,并且表示直线的单位方向向量也完全重合, 则这时必有如下关系成立  
(3)
$$
\mathbf{n}_2 = R\mathbf{n}_1
$$
根据直线变换后完全重合的条件有  
(4)
$$
\begin{aligned}
R\mathbf{p}_1+\mathbf{t}&= R(\mathbf{n}_1\alpha + \mathbf{p}_1')+\mathbf{t}
\\
&=\mathbf{p}_2
\\
&= \mathbf{n}_2\beta + \mathbf{p}_2'
\\
&= R\mathbf{n}_1\beta+\mathbf{p}_2'
\\
&\Downarrow
\\
R\mathbf{n}_1(\beta-\alpha)&=R\mathbf{p}_1'+\mathbf{t} – \mathbf{p}_2'
\\
&\Downarrow
\\
(\beta-\alpha)\mathbf{a} &= \mathbf{b}
\end{aligned}
$$
上面的中间变量\(\mathbf{a}\)与 \(\mathbf{b}\)定义如下 
(5)
$$
\begin{aligned}
\mathbf{a} &= R \mathbf{n}_1
\\
\mathbf{b} &= R\mathbf{p}_1'+\mathbf{t} – \mathbf{p}_2'
\end{aligned}
$$
在公式(4)中，任意取一个\(\beta\)均有一个唯一对应的\(\alpha\).即个\(\beta-\alpha\)为一个常量,由于个\(\beta\)的任意性,很明显个\(\mathbf{a}\)与个\(\mathbf{b}\)满足如下关系  
(6)
$$
\dfrac{1}{|\mathbf{a}|}\mathbf{a}=\dfrac{1}{|\mathbf{b}|}\mathbf{b}
$$
虽然上面公式(6)可以直接构建约束,但由于涉及到向量取模,一种等效的方式是使用如下方程来约束  
(7)
$$
\begin{cases}
a_0b_1=a_1b_0
\\
a_0b_2=a_2b_0
\\
a_1b_2=a_2b_1
\end{cases}
$$
公式(7)中有效约束实际为2个方程，实际使用时，可以任意选则两个方程进行构建。很明显，公式(7)的计算量比公式(6)小了很多，因此实际情况下可使用公式(7)来构建约束。

另一种方式是使用如下方式构建，针对公式(4)有  
(8)
$$\begin{aligned}
R\mathbf{n}_1(\beta-\alpha)&=R\mathbf{p}_1'+\mathbf{t} – \mathbf{p}_2'
\\
&\Downarrow
\\
\mathbf{p}_2'^\wedge R\mathbf{n}_1(\beta-\alpha) &= \mathbf{p}_2'^\wedge (R\mathbf{p}_1'+\mathbf{t})
\\
&\Downarrow
\\
0 = (R\mathbf{n}_1)^T \mathbf{p}_2'^\wedge R\mathbf{n}_1(\beta-\alpha) &= (R\mathbf{n}_1)^T \mathbf{p}_2'^\wedge (R\mathbf{p}_1'+\mathbf{t}) \end{aligned}$$
同理，可以得到如下约束表达式  
(9)
$$
\begin{cases}
(R\mathbf{n}_1)^T \mathbf{p}_2'^\wedge (R\mathbf{p}_1'+\mathbf{t}) = 0
\\
(R\mathbf{n}_1)^T \mathbf{t}^\wedge (R\mathbf{p}_1'-\mathbf{p}_2')=0
\end{cases}
$$

因此最终可以使用公式(3)与(7)来构建约束方程或者 (3)与(9)来构建约束方程。

1.2 不考虑方向向量匹配
有的情况下，我们无法保证提供的两个直线方向向量在变换后是否一致，这时，我们基于的理论是：A直线上的点变换后，一定在B直线上。则根据变换条件有  
(10)
$$
\begin{aligned}
R\mathbf{p}_1+\mathbf{t}&= R(\mathbf{n}_1\alpha + \mathbf{p}_1')+\mathbf{t}
\\
&=\mathbf{p}_2
\\
&= \mathbf{n}_2\beta + \mathbf{p}_2'
\\
&\Downarrow
\\
\mathbf{n}_2\beta&=\alpha R\mathbf{n}_1+R\mathbf{p}_1'+\mathbf{t} – \mathbf{p}_2'
\\
&\Downarrow
\\
\beta\mathbf{n}_2&=\alpha \mathbf{a} + \mathbf{b}
\\
&\Downarrow
\\
\beta \mathbf{b}^\wedge \mathbf{n}_2 &= \alpha \mathbf{b}^\wedge \mathbf{a}
\\
&\Downarrow
\\
\beta \mathbf{n}_2^T \mathbf{b}^\wedge \mathbf{n}_2 &= \alpha \mathbf{n}_2^T \mathbf{b}^\wedge \mathbf{a}
\\
&\Downarrow
\\
\mathbf{n}_2^T \mathbf{b}^\wedge \mathbf{a} &= 0
\end{aligned}
$$
即从(10)中我们可以得到一个约束  
(11)
$$
\mathbf{n}_2^T \mathbf{b}^\wedge \mathbf{a} = 0
$$
虽然(11)算式反应了两条直线匹配的关系，但是还有一个隐藏约束没有用到，即两条直线上的点一一对应。即，每个\(\beta\)对应着一个唯一的 \(\alpha\)，上面公式在约去\(\beta\)的过程中，并没有反映其一一对应性，为了进一步找出约束关系，这里设  
(12)
$$
\mathbf{n}_2=\begin{bmatrix}
x
\\
y
\\
z
\end{bmatrix}
$$

1.2.1 消去x
当\(\mathbf{n}_2\)中绝对值元素最大的值为\(x\),则消去(10)中的\(\beta\)有  
(13)
$$
\begin{aligned}
\begin{bmatrix}
\dfrac{y}{x}
\\
\\
\dfrac{z}{x}
\end{bmatrix}&=
\begin{bmatrix}
\dfrac{\alpha a_1+b_1}{\alpha a_0 + b_0}
\\
\\
\dfrac{\alpha a_2+b_2}{\alpha a_0 + b_0}
\end{bmatrix}
\\
&\Downarrow
\\
&\begin{cases}
\alpha(a_0y-a_1x)+(b_0y-b_1x)=0
\\
\alpha(a_0z-a_2x) +(b_0z-b_2x)=0
\end{cases}
\end{aligned}
$$
由于每个\(\beta\)对应着唯一的\(\alpha\), 当\(\beta\)取任意值时,\(\alpha\)也可以看成可取任意值.由于\(\beta\)取任意值均需要满足上面表达式,则可以得到如下约束方程  
(14)
$$
\begin{cases}
a_0y=a_1x
\\
b_0y=b_1x
\\
a_0z=a_2x
\\
b_0z=b_2x
\end{cases}
$$
上面公式中隐含了 \(a_0b_1=a_1b_0\)与 \(a_0b_2=a_2b_0\)。因此最终使用(14)算式构建约束。

1.2.2 消去y
当\(\mathbf{n}_2\)中绝对值元素最大的值为\(y\),则消去(10)中的\(\beta\)有  
(15)
$$
\begin{aligned}
\begin{bmatrix}
\dfrac{x}{y}
\\
\\
\dfrac{z}{y}
\end{bmatrix}&=
\begin{bmatrix}
\dfrac{\alpha a_0+b_0}{\alpha a_1 + b_1}
\\
\\
\dfrac{\alpha a_2+b_2}{\alpha a_1 + b_1}
\end{bmatrix}
\\
&\Downarrow
\\
&\begin{cases}
\alpha(a_1x-a_0y)+(b_1x-b_0y)=0
\\
\alpha(a_1z-a_2y) +(b_1z-b_2y)=0
\end{cases}
\end{aligned}
$$
由于每个\(\beta\)对应着一个\(\alpha\), 当\(\beta\)取任意值时,\(\alpha\)也可以看成可取任意值.由于\(\beta\)取任意值均需要满足上面表达式,则可以得到如下约束方程  
(16)
$$
\begin{cases}
a_1x=a_0y
\\
b_1x=b_0y
\\
a_1z=a_2y
\\
b_1z=b_2y
\end{cases}
$$
上面公式中隐含了 \(a_0b_1=a_1b_0\)与 \(a_1b_2=a_2b_1\)。因此最终使用(16)算式构建约束。

1.2.3 消去z
当\(\mathbf{n}_2\)中绝对值元素最大的值为\(z\),则消去(10)中的\(\beta\)有  
(17)
$$
\begin{aligned}
\begin{bmatrix}
\dfrac{x}{z}
\\
\\
\dfrac{y}{z}
\end{bmatrix}&=
\begin{bmatrix}
\dfrac{\alpha a_0+b_0}{\alpha a_2 + b_2}
\\
\\
\dfrac{\alpha a_1+b_1}{\alpha a_2 + b_2}
\end{bmatrix}
\\
&\Downarrow
\\
&\begin{cases}
\alpha(a_2x-a_0z)+(b_2x-b_0z)=0
\\
\alpha(a_2y-a_1z) +(b_2y-b_1z)=0
\end{cases}
\end{aligned}
$$
由于每个\(\beta\)对应着一个\(\alpha\), 当\(\beta\)取任意值时,\(\alpha\)也可以看成可取任意值.由于\(\beta\)取任意值均需要满足上面表达式,则可以得到如下约束方程  
(18)
$$
\begin{cases}
a_2x=a_0z
\\
b_2x=b_0z
\\
a_2y=a_1z
\\
b_2y=b_1z
\end{cases}
$$
上面公式中隐含了 \(a_0b_2=a_2b_0\)与 \(a_1b_2=a_2b_1\)。因此最终使用(18)算式构建约束。