MathSword教程11. 二维振动-多峰拟合

1 背景

在研究工作中，可能会遇到：① 二维多峰函数拟合；② 二维带多个振动项函数拟合；③ 二维带趋势项函数拟合。更有甚者是这三种类型的组合。为了便于这几种模型求解，MathSword提供三种模型的组合模型，具体公式如下

（1-1）

$$\begin{aligned}x(t)&=\underbrace{\alpha+\sum_{i=1}^{n_1}a_it^i}_{趋势项}\\&+\underbrace{\sum_{i=1}^{n_2}\exp(-\beta_it)(b_i+g_it)+\sum_{i=1}^{n_3}(d_i\exp(-\gamma_it)+e_i)\cos(w_it+r_i)}_{振动项}\\&+\underbrace{\sum_{i=1}^{n_4}\dfrac{2h_i}{\pi}\dfrac{p_i}{4(t-c_i)^2+ p_i^2} + \sum_{i=1}^{n_5}\dfrac{q_i}{\sigma_i\sqrt{2\pi}}\exp(-\dfrac{(t-u_i)^2}{2\sigma_i^2})+\sum_{i=1}^{n_6}\mathbf{unsymSin}(t,A_i,s_i,w_{li},w_{ri})}_{多峰项}\end{aligned}$$

上面的模型具有如下特色:

（1) 支持三种数学模型的组合模型(趋势项、振动项、多峰项)，在实际拟合时可以单独设置某一类、或者某几类函数模型。

  (2) 每一类函数均可通过各自的求和系数\(n\)设置多次同类型函数累加。

（3) 振动项函数尽量统一常见的阻尼衰减以及来回振动函数。

  (4) 多峰函数由高斯函数、洛伦兹函数以及自定义的非对称正弦函数\(\mathbf{unsymSin}\)构成，其中非对称正弦函数定义如下:

（1-2）

$$\mathbf{unsymSin}(t,A,s,w_l,w_r)=\begin{cases}0&,t < s-w_l\\ \dfrac{A}{2}(1+\sin(\dfrac{t-s}{w_l}\pi+\dfrac{\pi}{2}))&, s-w_l \leq t < s \\ \dfrac{A}{2}(1-\sin(\dfrac{t-s}{w_r}\pi-\dfrac{\pi}{2}))&,s \leq t <s+w_r \\ 0&, t \geq s+ w_r  \end{cases}$$

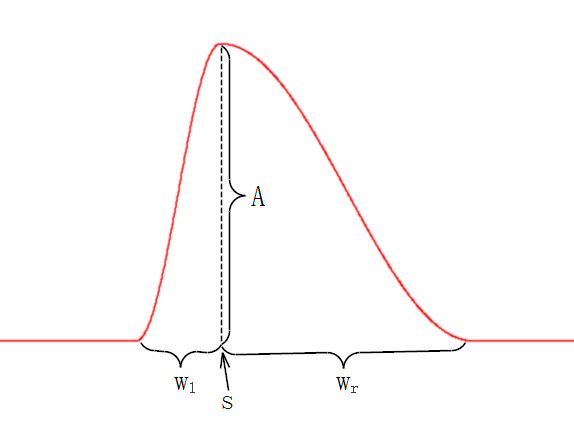
如下图，上面公式里\(A, s,  w_l, w_r\)分别表示波的幅值、波峰(波谷)处位置、左半轴大小、右半轴大小。

 （5）在拟合时，如果拟合效果不如意，注意数据量是否足够，以及可以【数据】里的变量增加一列(第3列)设置权重。

 （6）对于多峰拟合，在观测到各个峰可能所在的中心后，建议优先设置各个峰中心的优化范围。比如设置上面参数\(c,u,s\)的范围。

2 教程

MathSword里提供【2D振动-多峰拟合】工具箱对上面的数学模型进行设置，拟合后可以得到模型对象，进而可以通过模型对象进行参数求解、模型参数获取。